62 Model Selection and Checking - Practical

62.1 Introduction

In time series analysis, ‘models’ are mathematical representations that describe the underlying structure and behavior of time-dependent data.

As we’ve learned, they aim to capture and explain the inherent patterns within the data (trend, seasonality, and cyclical variations), enabling us to perform forecasting and explore causal influence.

Common models include ARIMA (AutoRegressive Integrated Moving Average), SARIMA (Seasonal ARIMA), and more advanced machine learning approaches like LSTM (Long Short-Term Memory) networks.

Our choice of model is important and depends on the specific characteristics of the data, such as its stationarity, seasonality, and noise. In this section we’ll review proper model selection, fitting, and validation.

62.2 Model selection: demonstration

Step One: Creating a dataset

First, we’ll create a dataframe called df from the stepcount data at the following link:

Show code

rm(list=ls())

df <- read.csv('https://www.dropbox.com/scl/fi/2zbxksqqv2igj3vq3hnh3/step_counts.csv?rlkey=t22p8s0wuzqbolewc0yph1m17&dl=1')

Now, we’ll convert that to a time series object. The stepcount data has been collected daily, so I’ll use the xts package.

As the dataset doesn’t include dates, I’ll need to add those as well (xts requires this information).

Show code

# Load library
library(xts)

Loading required package: zoo


Attaching package: 'zoo'

The following objects are masked from 'package:base':

    as.Date, as.Date.numeric

Show code

# Create a sequence of 730 dates starting from January 1st, 2020
start_date <- as.Date("2020-01-01")
dates <- seq(from = start_date, by = "day", length.out = 730)

# Convert to an `xts` time-series object
df_xts <- xts(df, order.by = dates)

# Plot the time series
plot(df_xts, main = "Daily Step Counts", xlab = "Date", ylab = "Steps")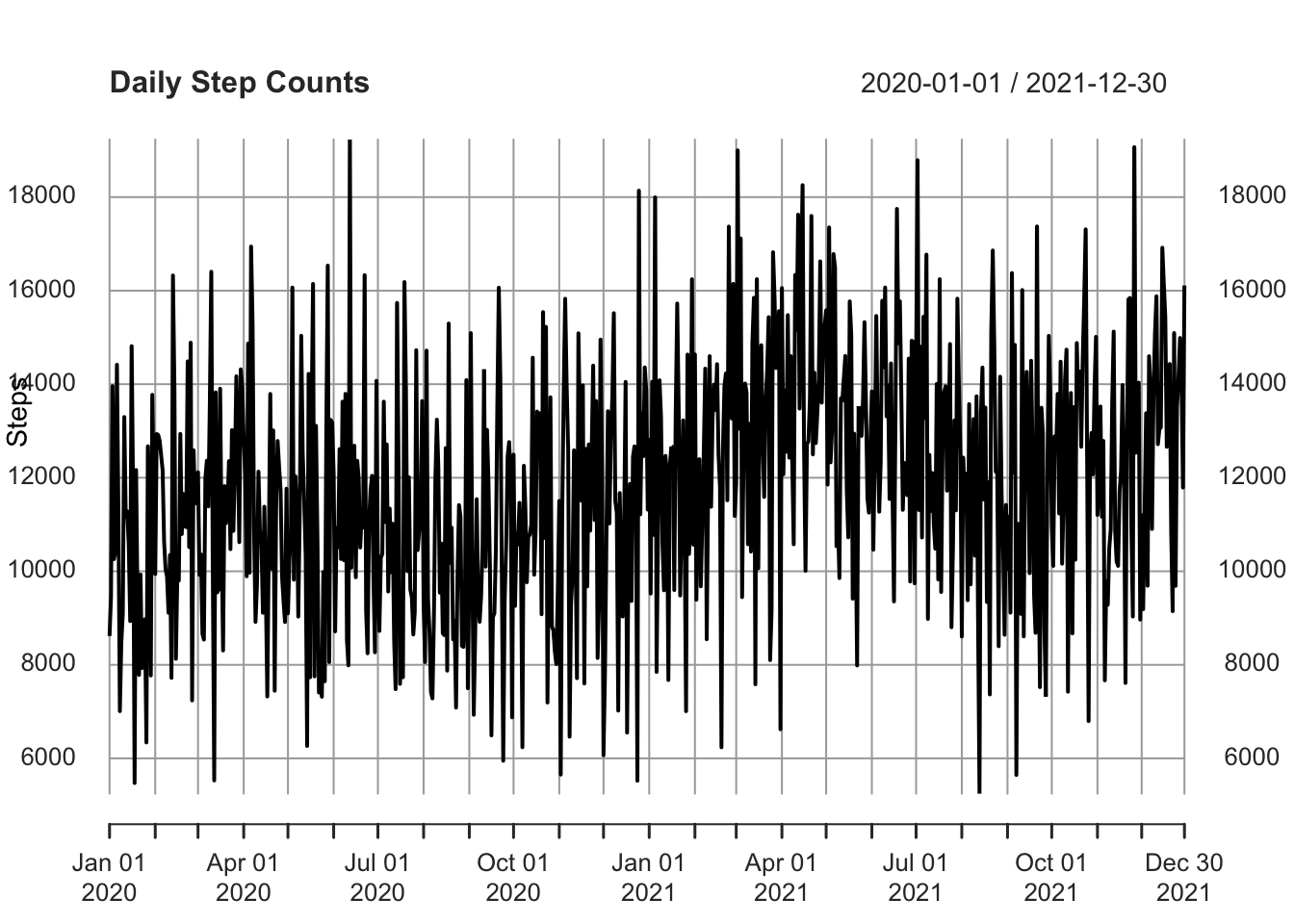

I’m going to decompose that time series, which is always good practice before doing anything more complicated.

Show code

ts_data <- ts(df_xts, frequency = 365) # convert to ts format

# Classical Decomposition
decomposed <- decompose(ts_data)
plot(decomposed)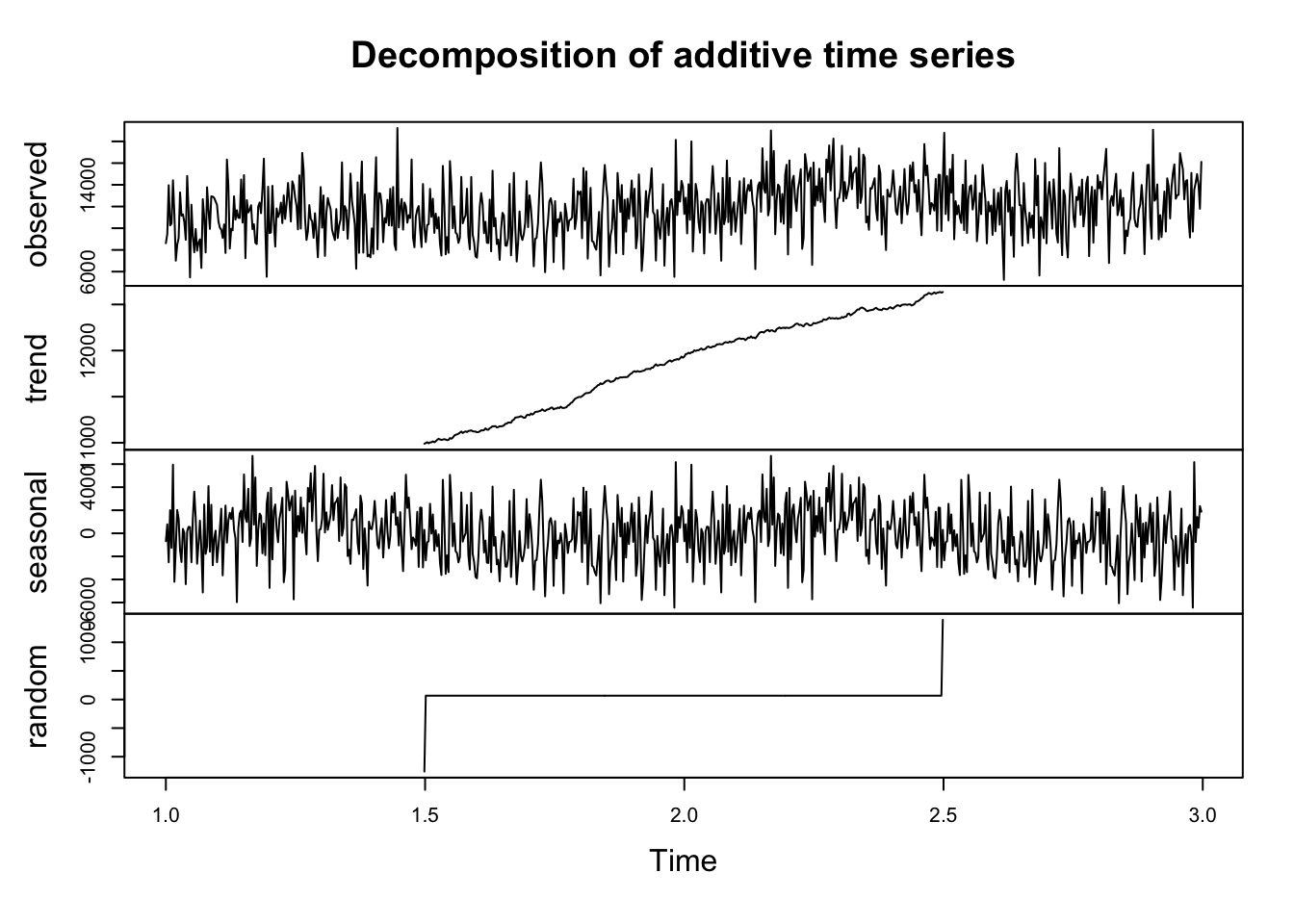

Step Two: Building some models

Now I’m going to build some predictive models.

Show code

# Load necessary libraries

library(xts)
library(forecast)

Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

First, I’ll build an Autoregressive model. Remember (from this week’s reading) that these models predict future values based on past values of the same variable. An AR model uses the dependence between an observation and a number of lagged observations.

AR models rely solely on their own previous values for forecasts. For example, we might predict an athlete’s performance tomorrow based on their performance over the last few days.

In the following code snippet, I create an AR model. The important part is that I enter max.q=0, which sets the moving average to 0. This means there is no moving average component in the model and hence it is an AR model.

# Fit an AR model
ar_model <- auto.arima(df_xts, max.p = 5, max.q = 0, seasonal = FALSE)
summary(ar_model)

Series: df_xts 
ARIMA(5,1,0) 

Coefficients:
          ar1      ar2      ar3      ar4      ar5
      -0.8477  -0.7124  -0.5096  -0.3345  -0.1593
s.e.   0.0366   0.0467   0.0501   0.0466   0.0366

sigma^2 = 7091095:  log likelihood = -6782.18
AIC=13576.36   AICc=13576.48   BIC=13603.91

Training set error measures:
                   ME     RMSE      MAE       MPE     MAPE     MASE        ACF1
Training set 22.85655 2651.945 2128.143 -4.784338 19.67236 0.765478 -0.02843993

Now I’ll plot that model:

library(ggplot2)

# Plot stepcount data
p <- ggplot(data = as.data.frame(df_xts), aes(x = index(df_xts), y = coredata(df_xts))) +
  geom_line(aes(y = coredata(df_xts)), color = "blue") +
  labs(title = "AR Model Visualisation", x = "Time", y = "Count")

# Add the fitted values
fitted_values <- fitted(ar_model)
p <- p + geom_line(aes(y = fitted_values), color = "red")

# Display the plot
print(p)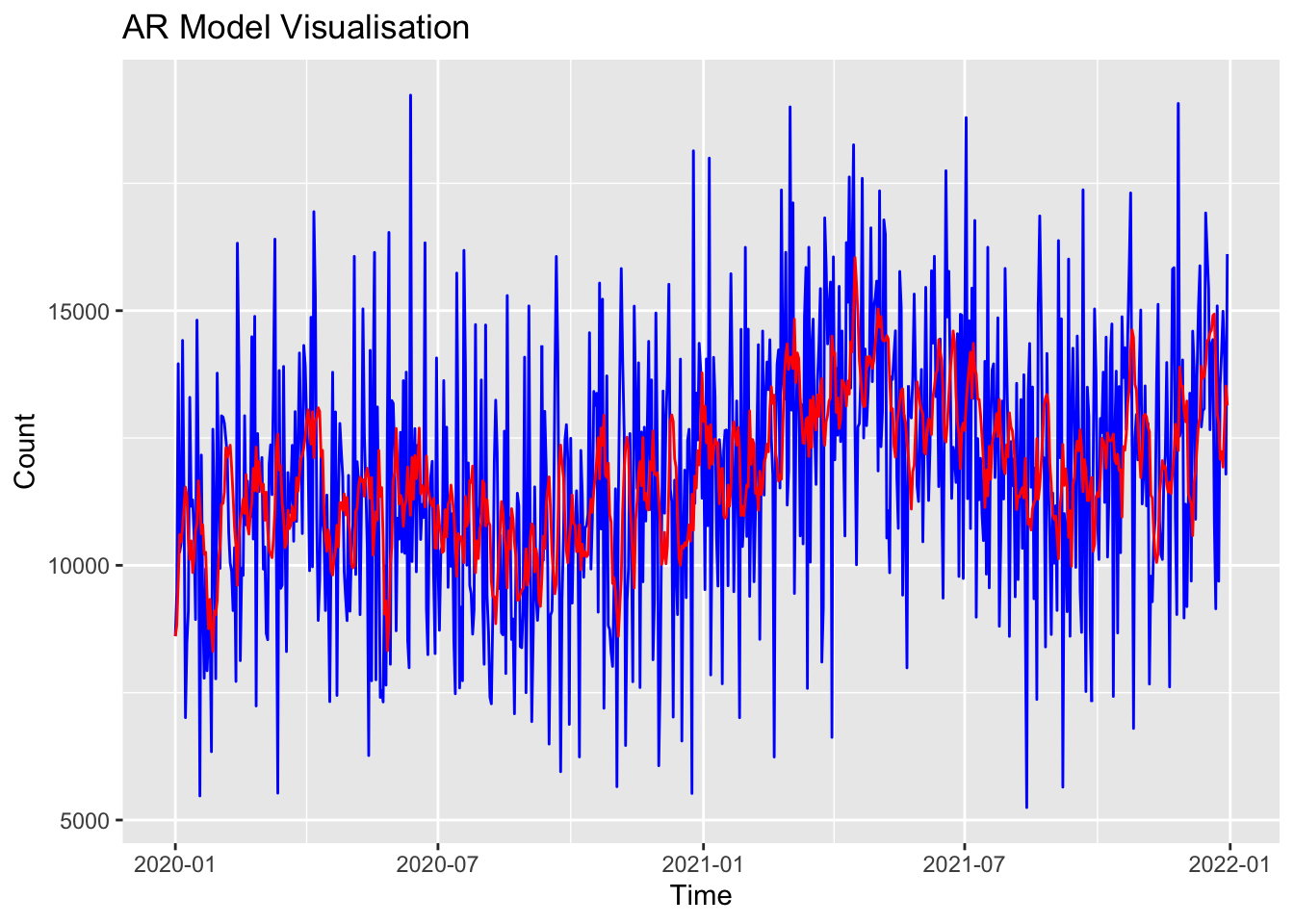

A second option is an MA model. Here, the moving average (q) is set to 5, and the autoregressive component is set to 0. This means the model is only using the moving average.

# Fit an MA model
ma_model <- auto.arima(df_xts, max.p = 0, max.q = 5, seasonal = FALSE)
summary(ma_model)

Series: df_xts 
ARIMA(0,1,1) 

Coefficients:
          ma1
      -0.9622
s.e.   0.0089

sigma^2 = 6146893:  log likelihood = -6732.87
AIC=13469.75   AICc=13469.76   BIC=13478.93

Training set error measures:
                   ME     RMSE      MAE     MPE    MAPE      MASE        ACF1
Training set 94.73032 2475.894 1987.373 -4.0905 18.3443 0.7148437 -0.03965665

I can plot that MA model to see how it performs relative to the ‘real’ data:

# Plot stepcount data
p <- ggplot(data = as.data.frame(df_xts), aes(x = index(df_xts), y = coredata(df_xts))) +
  geom_line(aes(y = coredata(df_xts)), color = "blue") +
  labs(title = "MA Model Visualisation", x = "Time", y = "Count")

# Add the fitted values
fitted_values <- fitted(ma_model)
p <- p + geom_line(aes(y = fitted_values), color = "red")

# Display plot
print(p)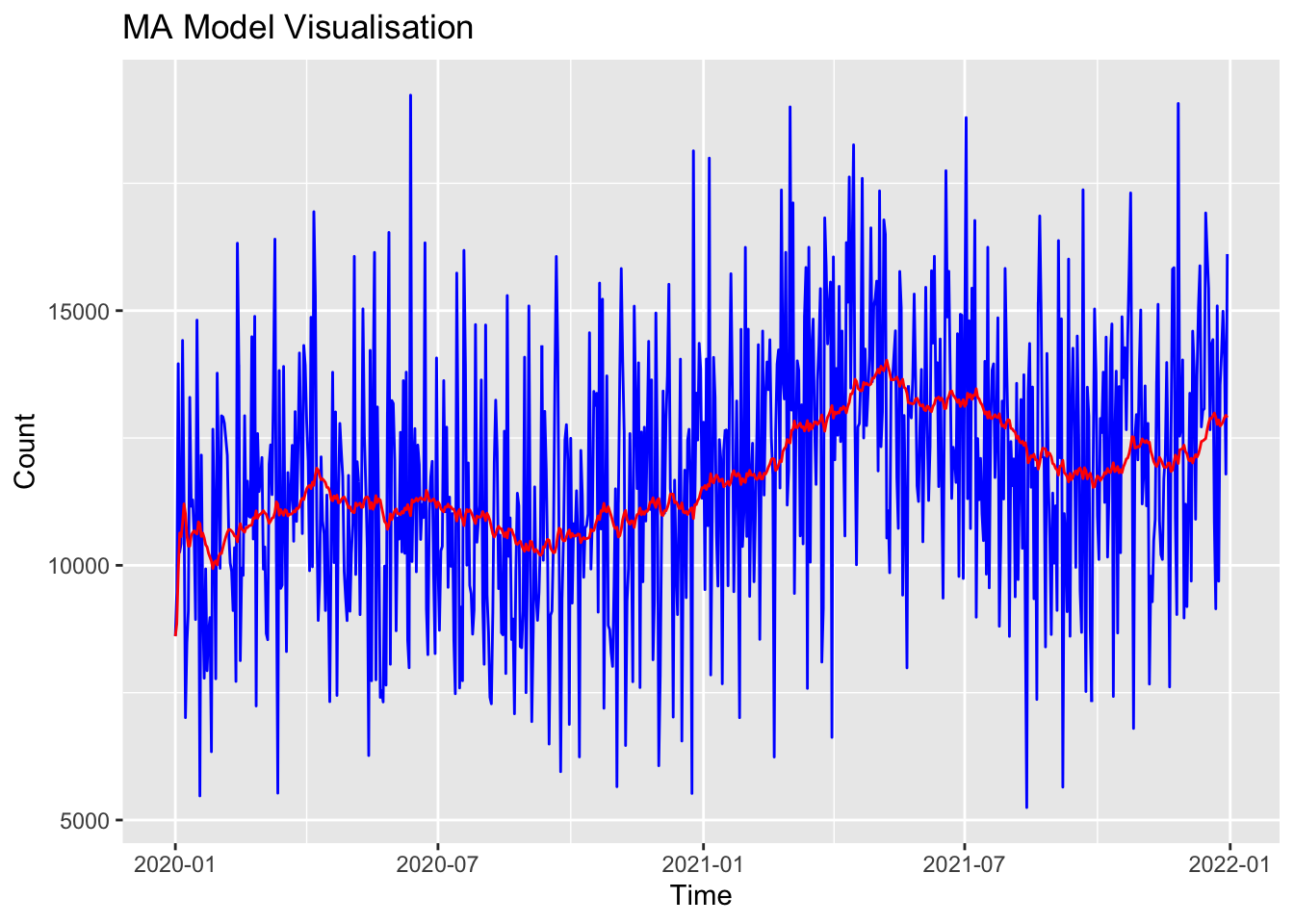

The ARIMA model is an extension of ARMA models that also include differencing of observations to make a non-stationary time series stationary. This process allows them to handle data with trends over time.

# Fit an ARIMA model
arima_model <- auto.arima(df_xts)
summary(arima_model)

Series: df_xts 
ARIMA(1,1,2) 

Coefficients:
         ar1      ma1    ma2
      0.7178  -1.7377  0.750
s.e.  0.1520   0.1397  0.134

sigma^2 = 6123110:  log likelihood = -6730.51
AIC=13469.01   AICc=13469.07   BIC=13487.38

Training set error measures:
                   ME     RMSE      MAE       MPE     MAPE      MASE       ACF1
Training set 88.19725 2467.703 1981.442 -4.107803 18.28573 0.7127106 0.01238791

I can plot that ARIMA model to see how it performs relative to the ‘real’ data:

# Plot stepcount data
p <- ggplot(data = as.data.frame(df_xts), aes(x = index(df_xts), y = coredata(df_xts))) +
  geom_line(aes(y = coredata(df_xts)), color = "blue") +
  labs(title = "ARIMA Model Visualisation", x = "Time", y = "Count")

# Add the fitted values
fitted_values <- fitted(arima_model)
p <- p + geom_line(aes(y = fitted_values), color = "red")

# Display plot
print(p)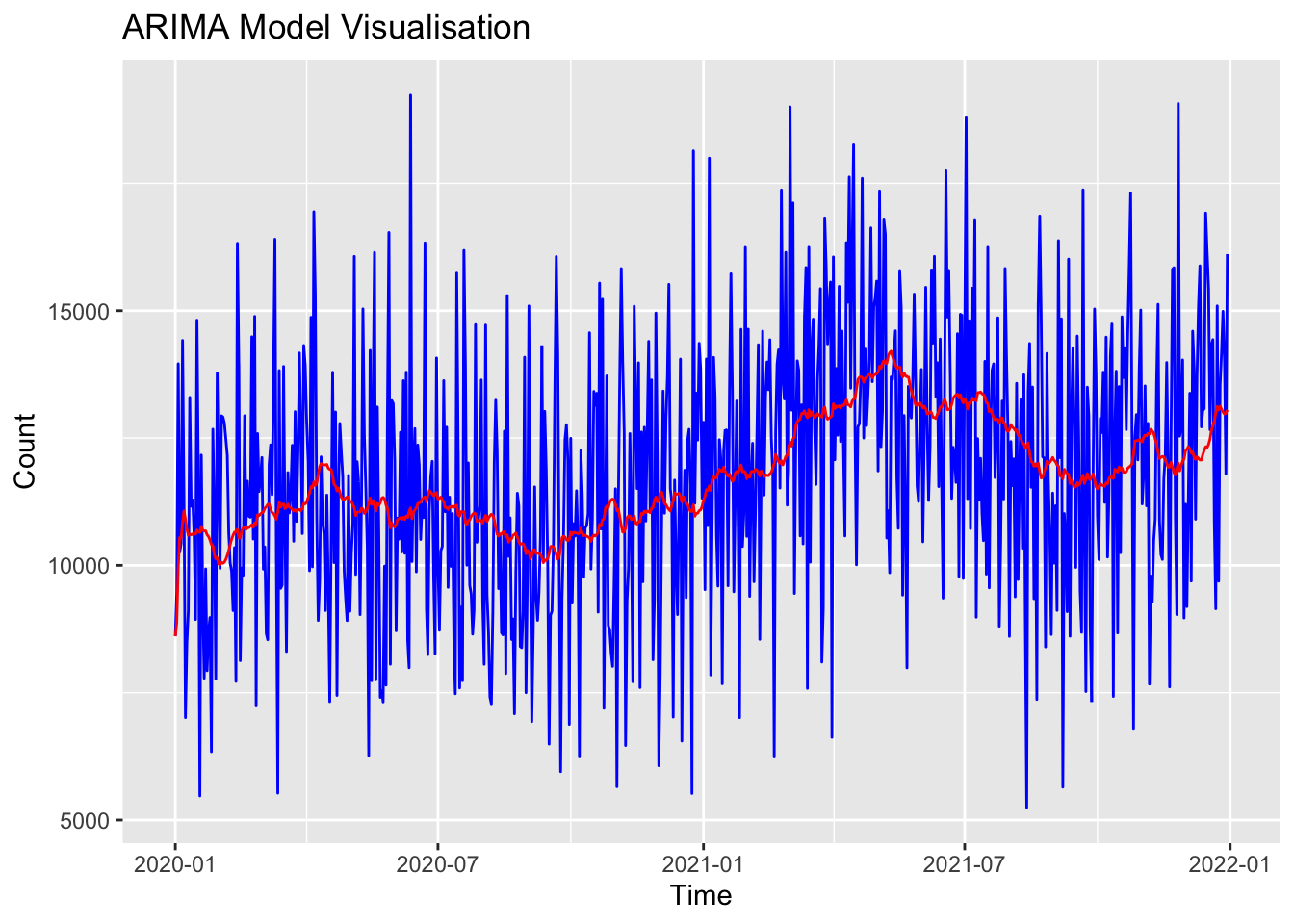

Finally, I’ll calculate an Exponential Smoothing model. These models apply smoothing factors to make forecasts. They’re useful because they easily adjust to data trends and seasonal patterns by applying more weight to more recent observations.

# Fit an Exponential Smoothing State Space Model (ETS)
ets_model <- ets(df_xts)
summary(ets_model)

ETS(A,N,N) 

Call:
 ets(y = df_xts) 

  Smoothing parameters:
    alpha = 0.0368 

  Initial states:
    l = 10664.555 

  sigma:  2479.27

     AIC     AICc      BIC 
16227.87 16227.90 16241.65 

Training set error measures:
                   ME     RMSE      MAE       MPE     MAPE     MASE        ACF1
Training set 87.19509 2475.872 1991.321 -4.172944 18.39359 0.716264 -0.03956356

# Plot stepcount data
p <- ggplot(data = as.data.frame(df_xts), aes(x = index(df_xts), y = coredata(df_xts))) +
  geom_line(aes(y = coredata(df_xts)), color = "blue") +
  labs(title = "ETS Model Visualisation", x = "Time", y = "Count")

# Add the fitted values
fitted_values <- fitted(ets_model)
p <- p + geom_line(aes(y = fitted_values), color = "red")

# Display plot
print(p)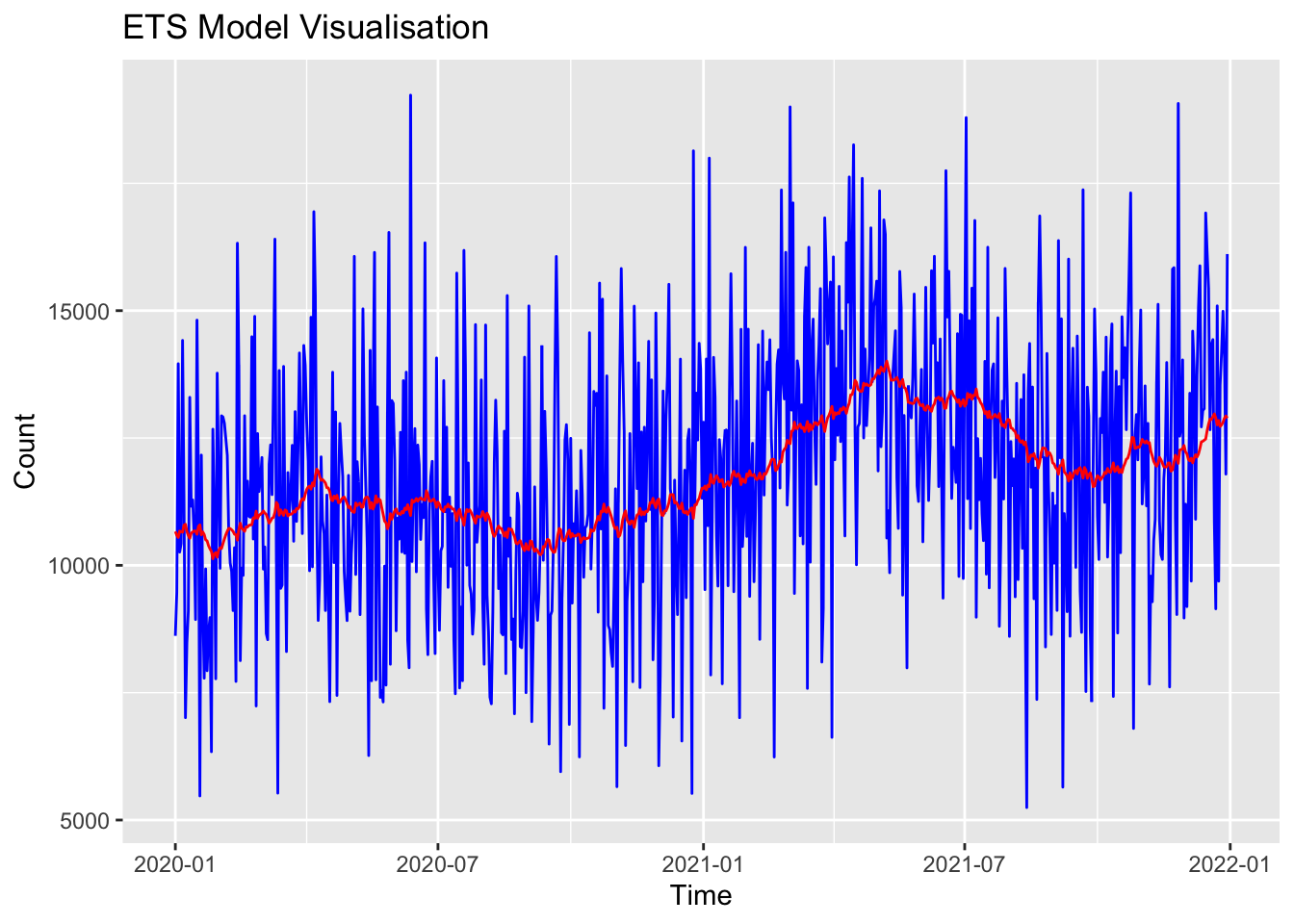

Step Three: Criterion-based selection

Now I have four different models that each attempts to predict future events based on historical time-series data; ar_model, ma_model, arima_model and ets_model.

I’d like to compare how these models ‘performed’ with my data, so I know which one I can rely on in the future.

The first approach we can use is criterion-based, where we use numerical information to compare models.

We noted previously that the most common metrics are AIC and BIC, so I’ll use them to evaluate how ‘good’ my models are:

Show code

checkresiduals(ar_model) # visual inspection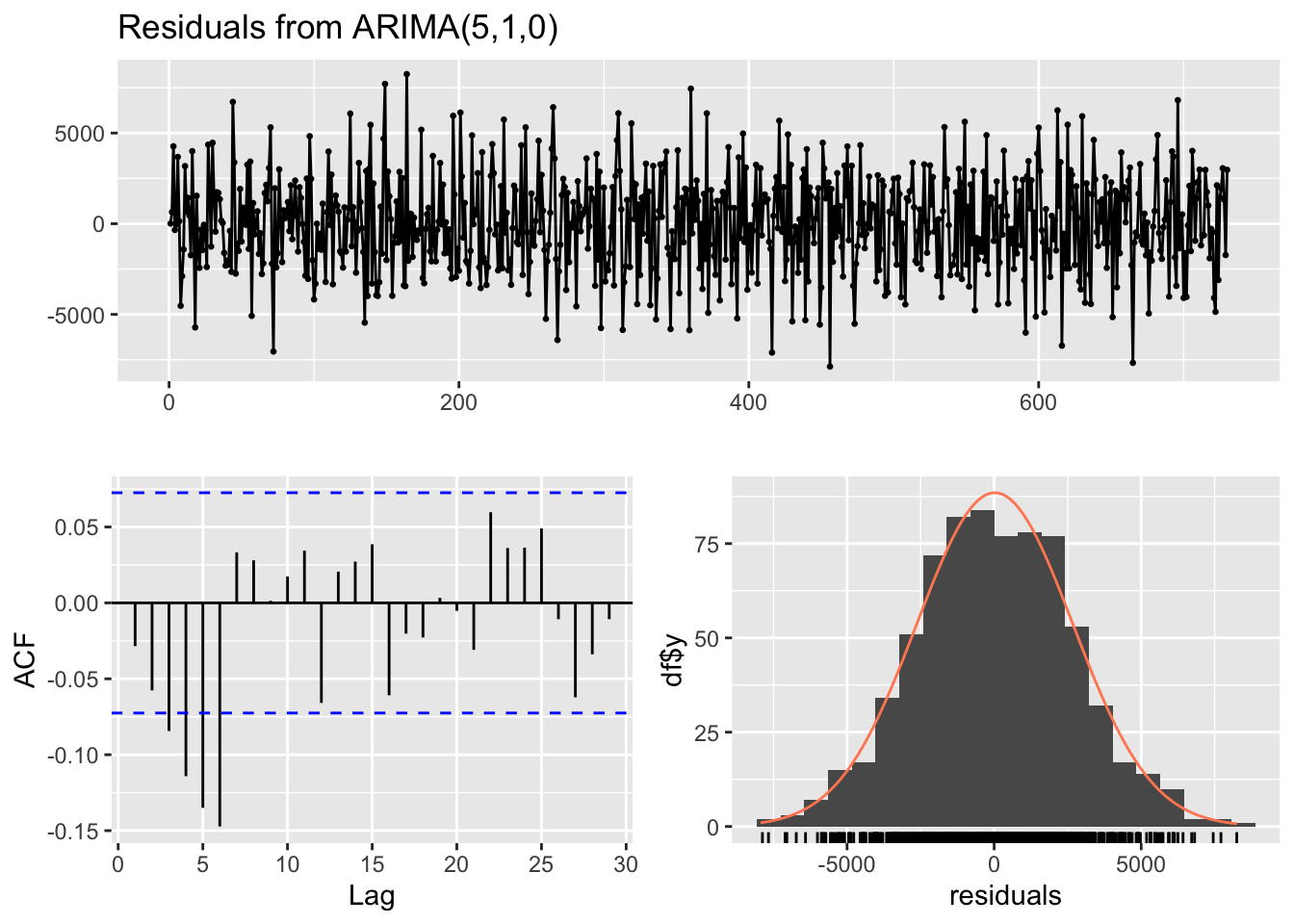


    Ljung-Box test

data:  Residuals from ARIMA(5,1,0)
Q* = 48.914, df = 5, p-value = 2.311e-09

Model df: 5.   Total lags used: 10

Show code

checkresiduals(ma_model) # visual inspection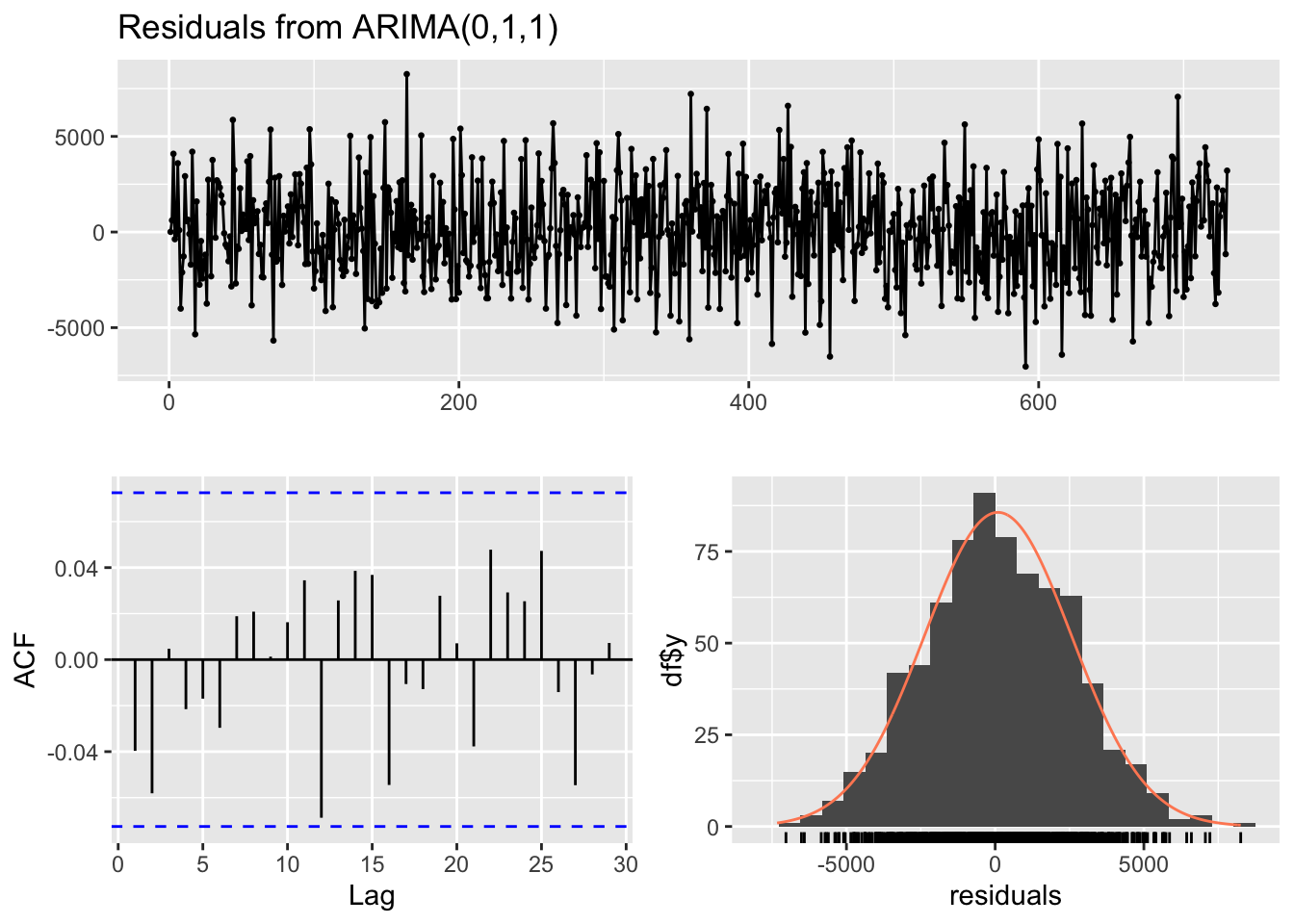


    Ljung-Box test

data:  Residuals from ARIMA(0,1,1)
Q* = 5.6318, df = 9, p-value = 0.7761

Model df: 1.   Total lags used: 10

Show code

checkresiduals(arima_model) # visual inspection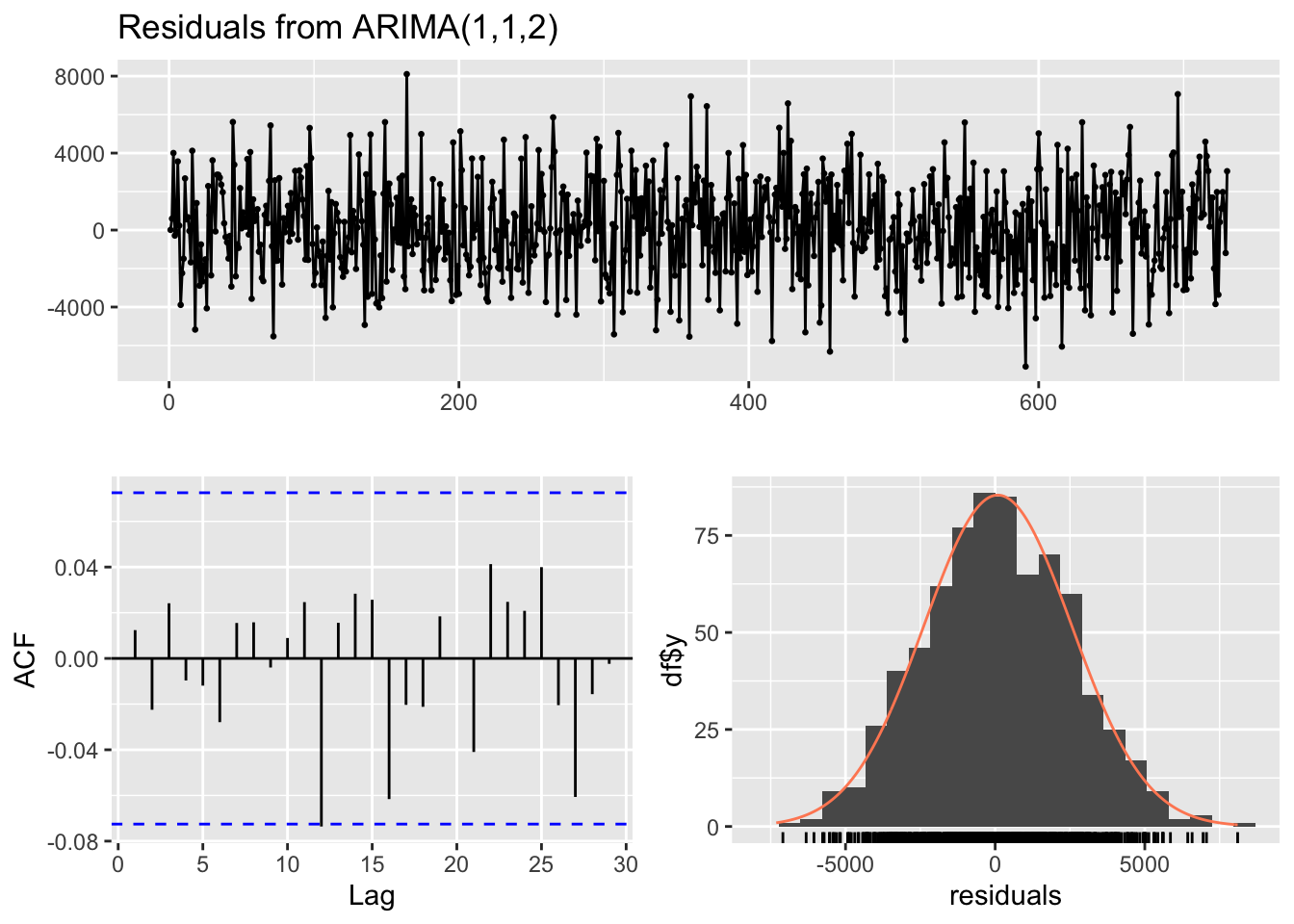


    Ljung-Box test

data:  Residuals from ARIMA(1,1,2)
Q* = 2.0936, df = 7, p-value = 0.9545

Model df: 3.   Total lags used: 10

Show code

checkresiduals(ets_model) # visual inspection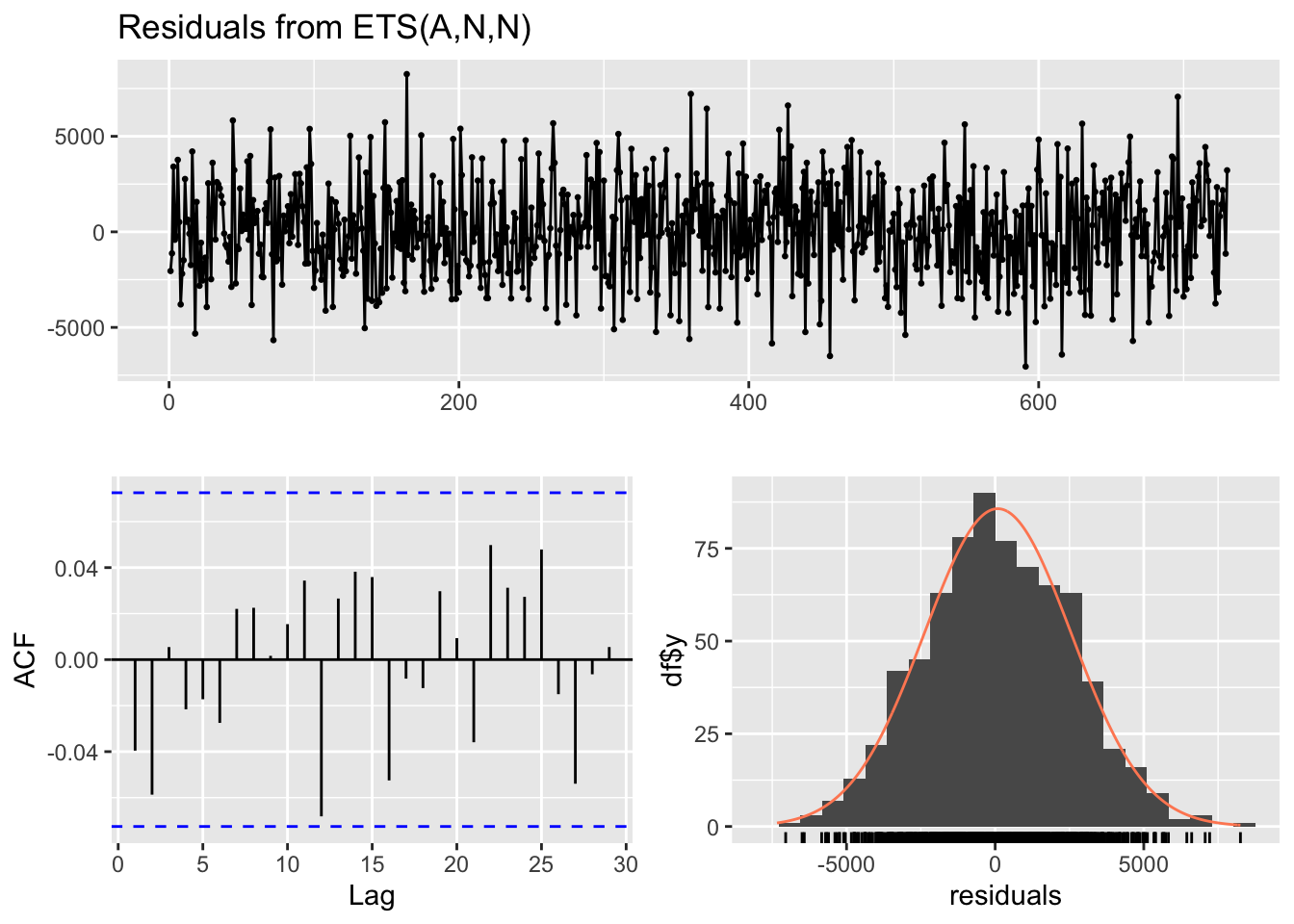


    Ljung-Box test

data:  Residuals from ETS(A,N,N)
Q* = 5.7332, df = 10, p-value = 0.8372

Model df: 0.   Total lags used: 10

Show code

print(arima_model$aic)

[1] 13469.01

Show code

print(arima_model$bic)

[1] 13487.38

Show code

print(ar_model$aic)

[1] 13576.36

Show code

print(ar_model$bic)

[1] 13603.91

Show code

# note that the AIC and BIC from the ARIMA model are lower than the AR model. This suggests that the ARIMA model is better.

print(ets_model$aic)

[1] 16227.87

Show code

print(ets_model$bic)

[1] 16241.65

Show code

print(ma_model$aic)

[1] 13469.75

Show code

print(ma_model$bic)

[1] 13478.93

Show code

# again, note that the ARIMA continues to out-perform the other models.

This analysis indicates that the ARIMA model and the MA model are ‘better’ than the others. All things considered, I would probably stick with the ARIMA model, and use that as the basis for my subsequent analysis. This is because it performed better on the AIC, which is a less stringent test and less likely to ‘fail’.

Step Four: Residual diagnostics

Alongside criterion-based methods, we can also use residual diagnostics to compare the effectiveness of different models.

Autocorrelation in residuals

In the previous section I mentioned using the Ljung-Box Q-test. We can use the following to produce this for each of our models.

Show code

# Assuming you have your four models: model1, model2, model3, model4

# Extract residuals from each model
residuals1 <- residuals(ar_model)
residuals2 <- residuals(arima_model)
residuals3 <- residuals(ets_model)
residuals4 <- residuals(ma_model)

# Apply the Ljung-Box test
ljung_box_result_ar <- Box.test(residuals1, type = "Ljung-Box")
ljung_box_result_arima <- Box.test(residuals2, type = "Ljung-Box")
ljung_box_result_ets <- Box.test(residuals3, type = "Ljung-Box")
ljung_box_result_ma <- Box.test(residuals4, type = "Ljung-Box")

# Print the results
print(ljung_box_result_ar)


    Box-Ljung test

data:  residuals1
X-squared = 0.59288, df = 1, p-value = 0.4413

Show code

print(ljung_box_result_arima)


    Box-Ljung test

data:  residuals2
X-squared = 0.11249, df = 1, p-value = 0.7373

Show code

print(ljung_box_result_ets)


    Box-Ljung test

data:  residuals3
X-squared = 1.1474, df = 1, p-value = 0.2841

Show code

print(ljung_box_result_ma)


    Box-Ljung test

data:  residuals4
X-squared = 1.1528, df = 1, p-value = 0.283

The function returns a test statistic and a p-value.

A high p-value (typically above 0.05) suggests that the residuals are independently distributed, which is a good indication that the model has adequately captured the information in the time series.n
Conversely, a low p-value might indicate that there is autocorrelation in the residuals, suggesting that the model may be missing some information from the data.

Note that the ARIMA output has the highest p-value, suggesting the residuals are independently distributed, and it is the ‘best’ type of model to use on this data. It confirms our analysis this model best accounts for the ‘time series’ nature of our data.

Homoscedasticity of Residuals

Remember: homoscedasticity implies that the residuals have constant variance across time. Heteroscedasticity, the opposite, suggests that the model’s error terms vary at different times, indicating that the model may not be equally effective across the entire dataset.

To check this in R we can carry out a number of different visual and statistical tests:

Show code

# Load packages
library(forecast)
library(tseries)
library(lmtest)
library(MASS)
library(FinTS)


Attaching package: 'FinTS'

The following object is masked from 'package:forecast':

    Acf

Show code

# Step 1: Visual Inspection of Residuals
residuals_arima <- residuals(arima_model)
ts.plot(residuals_arima, main="Residuals over Time", ylab="Residuals")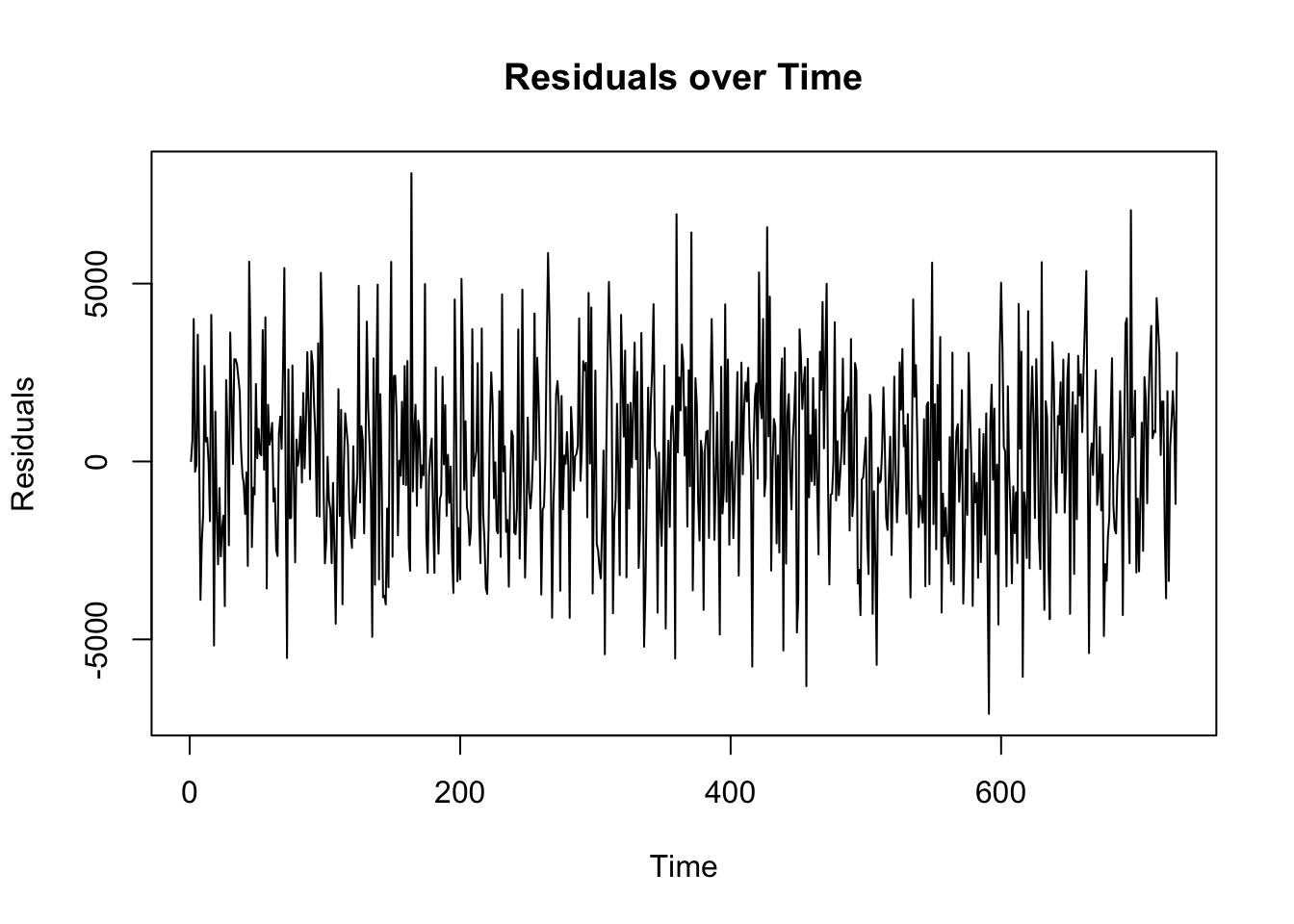

Show code

acf(residuals_arima, main="ACF of Residuals")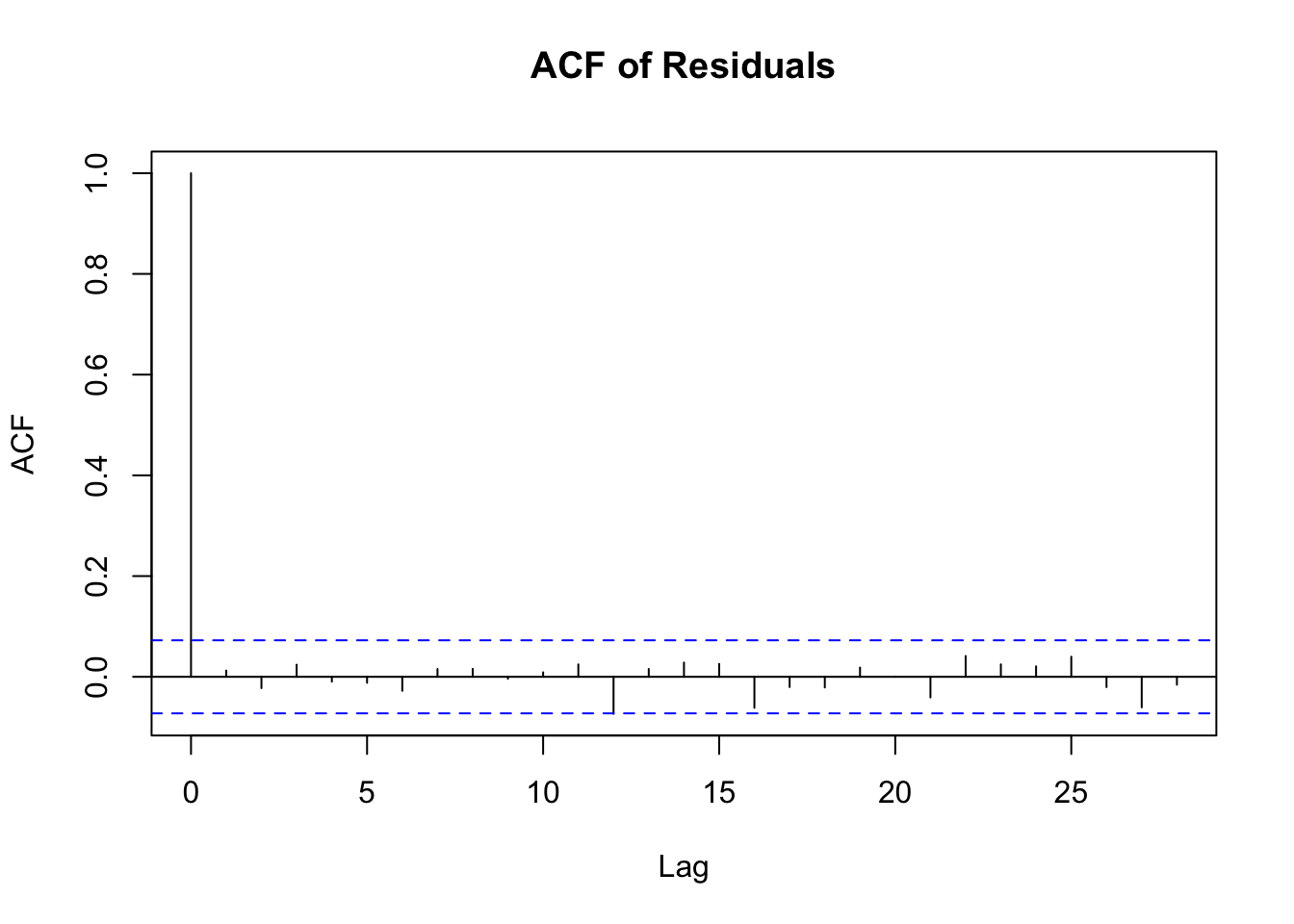

Show code

pacf(residuals_arima, main="PACF of Residuals")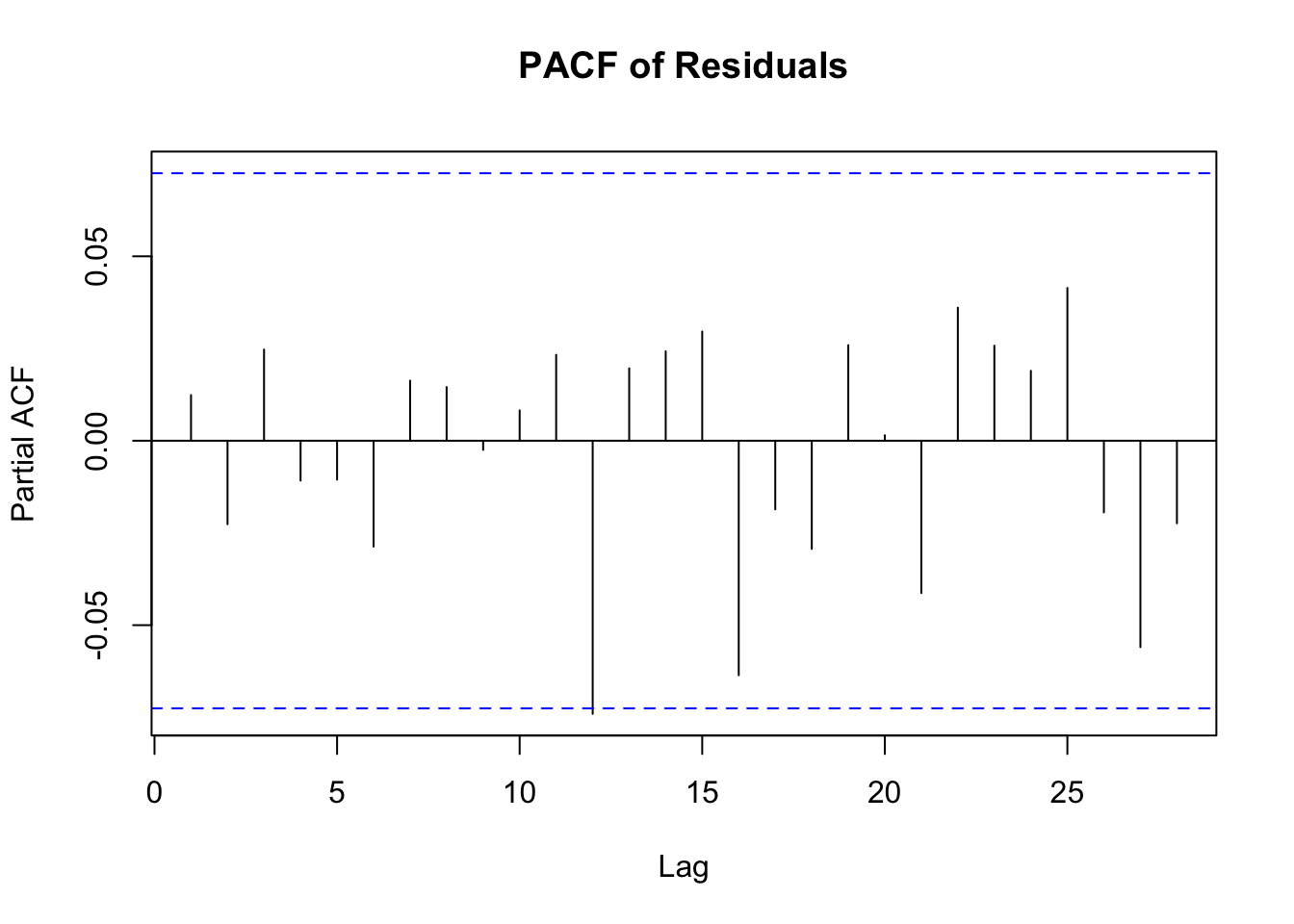

Show code

# Breusch-Pagan Test
bp_test <- bptest(residuals_arima ~ fitted(arima_model) + I(fitted(arima_model)^2))
print(bp_test)


    studentized Breusch-Pagan test

data:  residuals_arima ~ fitted(arima_model) + I(fitted(arima_model)^2)
BP = 3.0306, df = 2, p-value = 0.2197

Show code

# Goldfeld-Quandt Test
gq_test <- gqtest(residuals_arima ~ fitted(arima_model))
print(gq_test)


    Goldfeld-Quandt test

data:  residuals_arima ~ fitted(arima_model)
GQ = 1.0259, df1 = 363, df2 = 363, p-value = 0.4039
alternative hypothesis: variance increases from segment 1 to 2

Let’s examine that output.

Breusch-Pagan Test Interpretation The Breusch-Pagan test is used to detect heteroscedasticity in a regression model.

Null Hypothesis (H0): The variance of the errors is constant (homoscedasticity).
Alternative Hypothesis (H1): The variance of the errors is not constant (heteroscedasticity).
p-value: The key output of this test is the p-value.

If the p-value is low (commonly below 0.05), you reject the null hypothesis, suggesting the presence of heteroscedasticity. If the p-value is high, you fail to reject the null hypothesis, indicating no evidence of heteroscedasticity.

Goldfeld-Quandt Test Interpretation

The Goldfeld-Quandt test is another test for heteroscedasticity.

Null Hypothesis (H0): The variances of the errors in two separate groups (usually split based on an independent variable) are equal (no heteroscedasticity).
Alternative Hypothesis (H1): The variances of the errors in the two groups are different (heteroscedasticity).
p-value: Similar to the Breusch-Pagan test, the interpretation is based on the p-value.

A low p-value (typically <0.05) suggests rejecting the null hypothesis, indicating heteroscedasticity. A high p-value suggests failing to reject the null hypothesis, indicating no evidence of heteroscedasticity.

PACF Plot Interpretation

The Partial Autocorrelation Function (PACF) plot is used primarily to identify the order of an autoregressive (AR) model. Here’s how to interpret it:

Spikes in the Plot: The PACF plot shows the partial correlation of a time series with its own lagged values, controlling for the values of the time series at all shorter lags. Significant spikes (extending beyond the blue dashed lines, which represent confidence intervals) indicate a correlation with the lagged value at that particular lag.
Determining AR Order: The number of significant spikes starting from the origin gives an indication of the order of the AR model. For instance, if the first two lags have significant spikes and the rest are insignificant, an AR(2) model might be appropriate.
Cut-off after a Certain Lag: A sharp cut-off after a certain lag while the rest of the lags are insignificant (close to zero) is a typical indication of an AR process.

ACF Plot Interpretation

Y-Axis (Correlation): The ACF plot shows the correlation of a time series with its own lagged values. The y-axis represents the correlation coefficient, ranging from -1 to 1.
X-Axis (Lags): The x-axis represents the number of lags. Each bar (or spike) in the plot represents the correlation at a specific lag.
Significant Correlation: The blue dashed lines in the plot represent confidence intervals (usually set at 95%). If a bar extends beyond these lines, it indicates a statistically significant correlation at that lag.
- Interpreting Correlations:
  - Positive Correlation: If the bar is above the zero line, it indicates a positive correlation.
  - Negative Correlation: If the bar is below the zero line, it indicates a negative correlation. Determining Model Type:
Slow Decay: If the ACF shows a slow decay, it suggests a non-stationary series that might need differencing.
Sharp Drop after Lag k: If the ACF drops sharply after a certain lag k and then becomes insignificant, it may suggest an MA(k) model (Moving Average model of order k).
Seasonal Patterns: Repeated spikes at regular intervals suggest seasonality in the data.
Randomness: If all or most of the bars are within the confidence interval (not significantly different from zero), it suggests that the series is essentially random (white noise).

Normality of Residuals

Finally, as you know, the assumption of normality in residuals is central to many statistical inference techniques.
If the residuals are normally distributed, it suggests that the model has successfully captured the underlying data distribution, and the error term is purely random.

We can use a Q-Q plot to test this for each model, as follows. In the Q-Q plot, we can say the residuals are normally distributed if they sit close to the red line.

Show code

# Extract residuals
residuals_arima <- residuals(arima_model)

# Q-Q plot
qqnorm(residuals_arima)
qqline(residuals_arima, col = "red")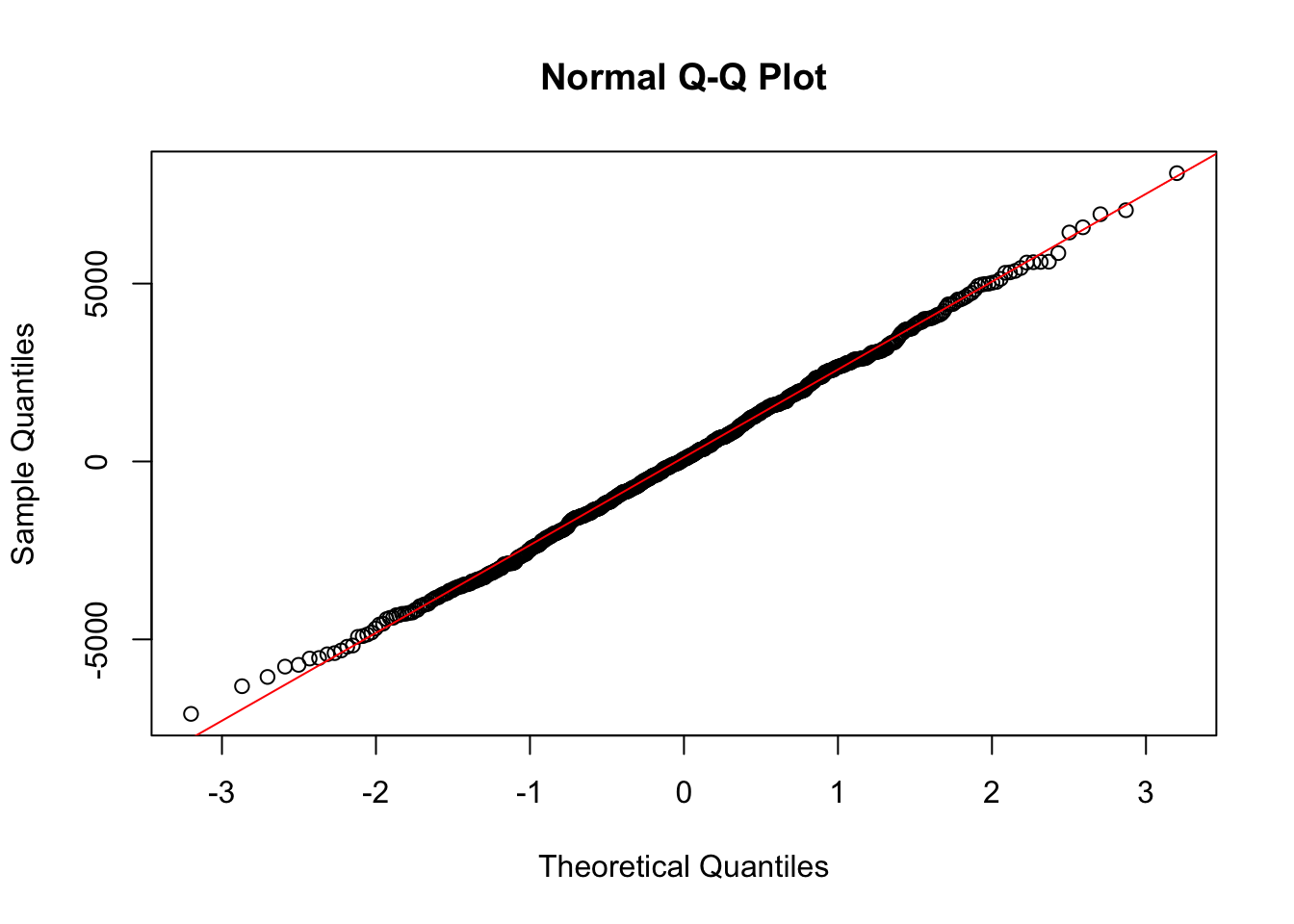

We can also carry out a Shapiro-Wilk test:

Show code

# Shapiro-Wilk normality test
shapiro_test <- shapiro.test(residuals_arima)
print(shapiro_test)


    Shapiro-Wilk normality test

data:  residuals_arima
W = 0.99862, p-value = 0.8522

Look at the p-value in the test output. - If the p-value is less than 0.05 (typical significance level), you reject the null hypothesis, an can assume that the residuals are not normally distributed. - If the p-value is greater than 0.05, you fail to reject the null hypothesis, and can assume that the residuals are normally distributed.

62.3 ARIMA and SARIMA Models

This was covered in the previous reading, but worth revising again as these are likely to be the types of models you will create most frequently.

ARIMA Models

ARIMA models (AutoRegressive Integrated Moving Average models) are frequently-used models in time-series analysis, especially for forecasting future trends based on past data. They help us predict future values in a sequence of data by analysing past values.

The “AR” part stands for AutoRegressive. The model looks at previous data points and uses these to predict future ones. It’s like trying to guess the next number in a sequence by looking at the numbers before it.
The “I” in ARIMA stands for Integrated. These models make the data more consistent and stable over time, often by removing trends or seasonal effects.
Lastly, the “MA” part stands for Moving Average. The models smooth out short-term fluctuations and highlight longer-term trends or cycles.

Seasonal ARIMA (SARIMA)

The SARIMA model is an extension of the ARIMA model, designed to better handle seasonal variations in time series data.

It’s structured to include both non-seasonal and seasonal elements. The full notation for a SARIMA model is SARIMA(p, d, q)(P, D, Q)m. Here’s what each of these components represents:

Non-Seasonal Components:

p (AutoRegressive Order): the number of lagged observations in the model. For instance, p = 2 would use the first two lagged values (like using data from the previous two months to predict this month’s value).
d (Integrated Order): the number of times the data needs to be differenced to make it stationary, meaning to stabilise the mean over time. For instance, if the data shows a linear trend, you might need to difference it once (d = 1) to remove that trend.
q (Moving Average Order): the size of the moving average window. It uses the error terms from the past forecasted values to improve the model’s accuracy.

Seasonal Components:

P (Seasonal AutoRegressive Order): similar to ‘p’, but for the seasonal part of the model. It represents the number of seasonal lags of the dependent variable that the model will use.
D (Seasonal Integrated Order): the number of seasonal differences required to make the series stationary.
Q (Seasonal Moving Average Order): similar to ‘q’, but for the seasonal part of the model. It represents the order of the moving average for the seasonal differences.
m (Seasonality Period): the number of time steps for a single seasonal period. For example, m = 12 for monthly data with an annual cycle.

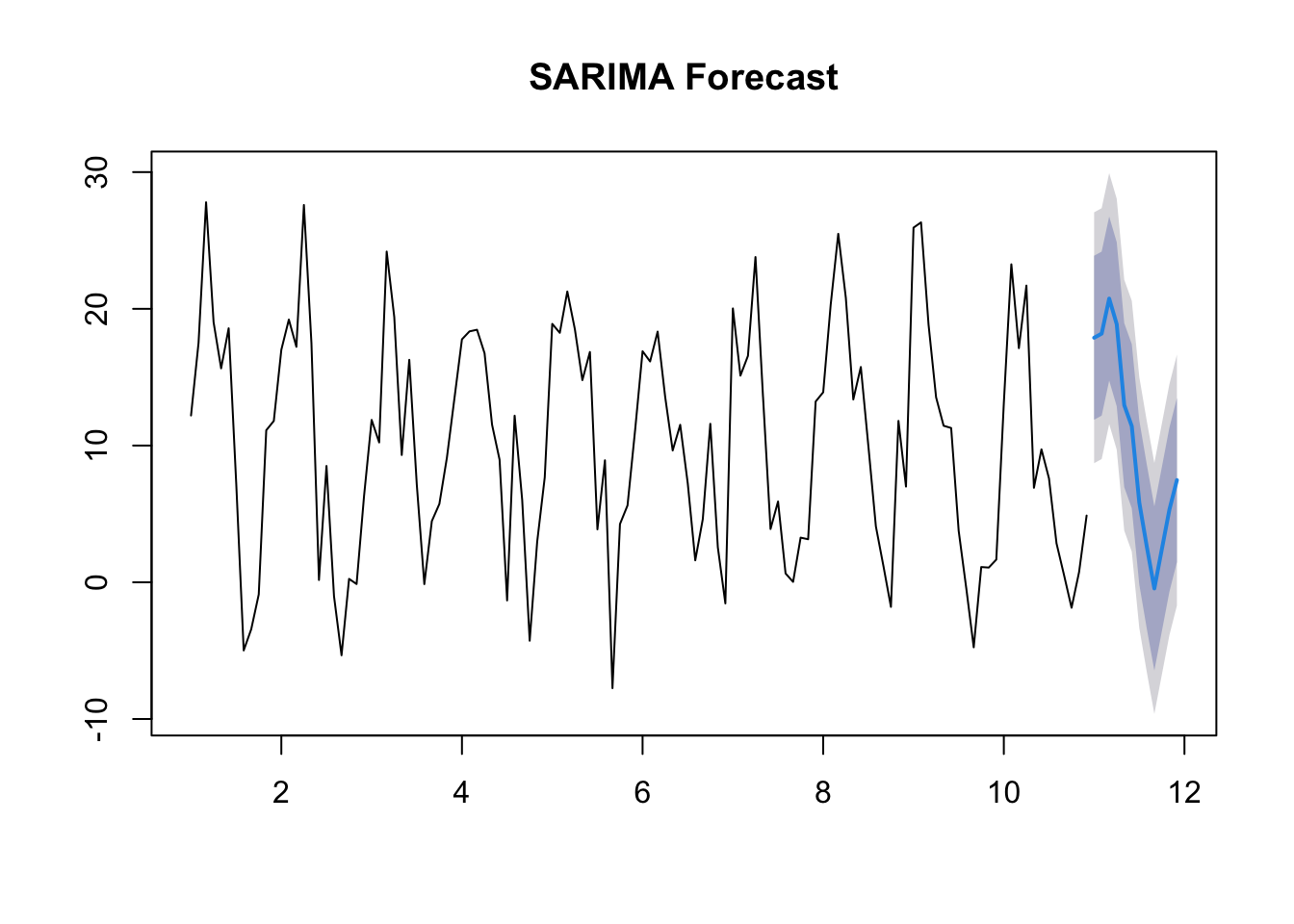
The strength of SARIMA models is their ability to decompose a series into seasonal and non-seasonal components and analyse these elements separately yet simultaneously, giving us a more accurate forecast in seasonally affected time-series data than ARIMA.

An example of ARIMA and SARIMA on the same dataset

In this example, I’ve created a dataset with a strong seasonal element.

Note that the output of ARIMA, which ignores the seasonal element, is less useful in terms of future forecasting than SARIMA, which takes the seasonal element into account.

The AIC for the SARIMA model is lower than that for the ARIMA model, indicating it is more effective.

Show code

# Load libraries
library(forecast)

# Create Dataset
set.seed(123)
seasonal_component <- sin(seq(1, 120, length.out = 120) * 2 * pi / 12) * 10
time_series_data <- ts(rnorm(120, mean = 10, sd = 5) + seasonal_component, frequency = 12)

# Plot dataset

plot(time_series_data, main = "Time-Series with Strong Seasonality", xlab = "Month", ylab = "Value")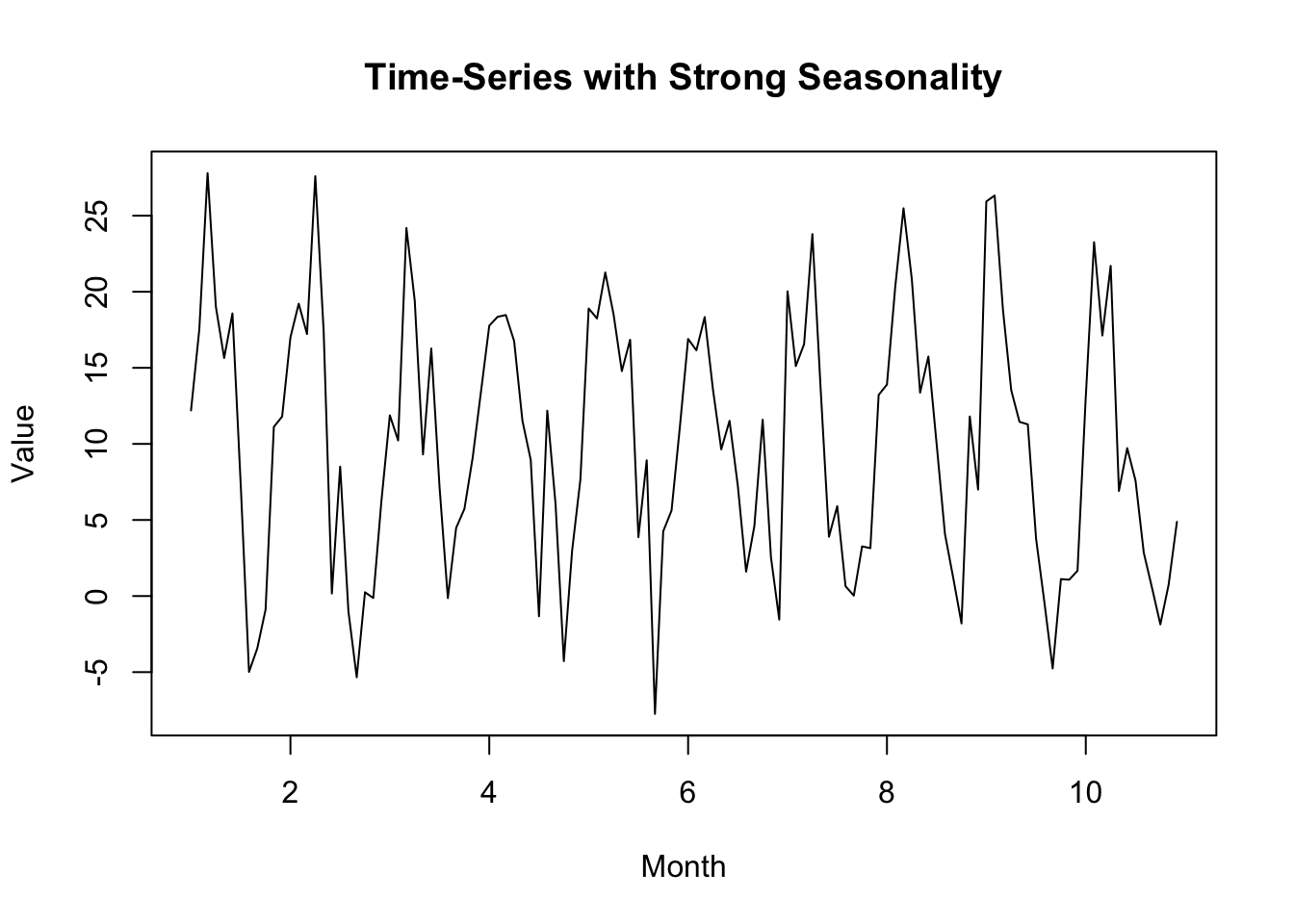

Show code

# ARIMA Model

arima_model <- auto.arima(time_series_data, seasonal = FALSE)
summary(arima_model)

Series: time_series_data 
ARIMA(1,0,0) with non-zero mean 

Coefficients:
         ar1     mean
      0.6204  10.0366
s.e.  0.0707   1.5384

sigma^2 = 42.74:  log likelihood = -394.82
AIC=795.64   AICc=795.85   BIC=804.01

Training set error measures:
                      ME     RMSE      MAE       MPE    MAPE     MASE
Training set -0.01512718 6.483211 5.120995 -99.28832 389.089 0.916242
                   ACF1
Training set 0.04754608

Show code

forecast_arima <- forecast(arima_model, h = 12)
plot(forecast_arima, main = "ARIMA Forecast")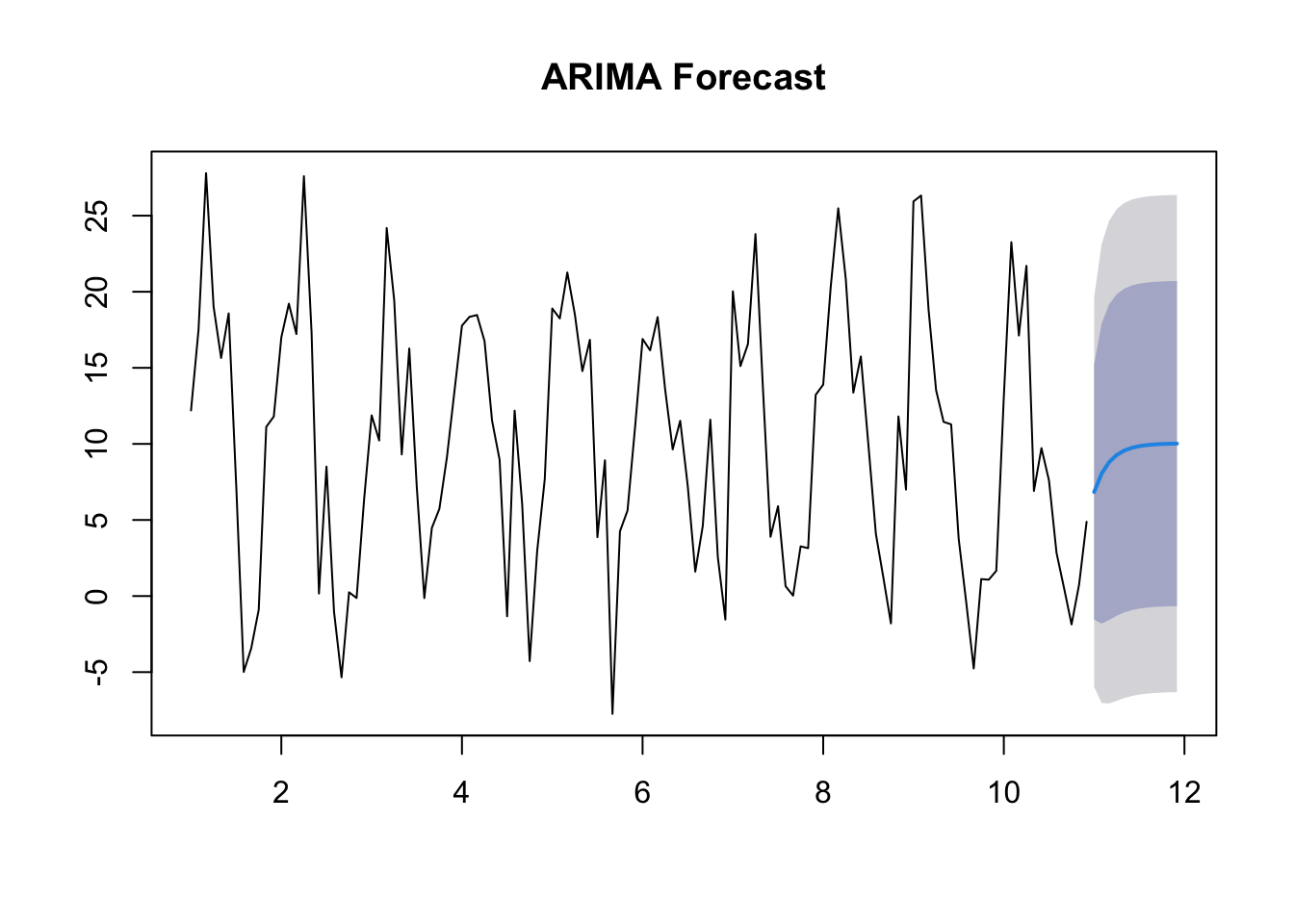

Show code

# SARIMA Model

sarima_model <- auto.arima(time_series_data, seasonal = TRUE)
summary(sarima_model)

Series: time_series_data 
ARIMA(0,0,0)(0,1,2)[12] 

Coefficients:
         sma1    sma2
      -1.0450  0.1803
s.e.   0.1533  0.1146

sigma^2 = 21.71:  log likelihood = -327.85
AIC=661.7   AICc=661.94   BIC=669.75

Training set error measures:
                     ME     RMSE     MAE      MPE    MAPE      MASE       ACF1
Training set -0.2040055 4.379059 3.28606 3.637575 226.066 0.5879376 0.04117254

Show code

forecast_sarima <- forecast(sarima_model, h = 12)
plot(forecast_sarima, main = "SARIMA Forecast")